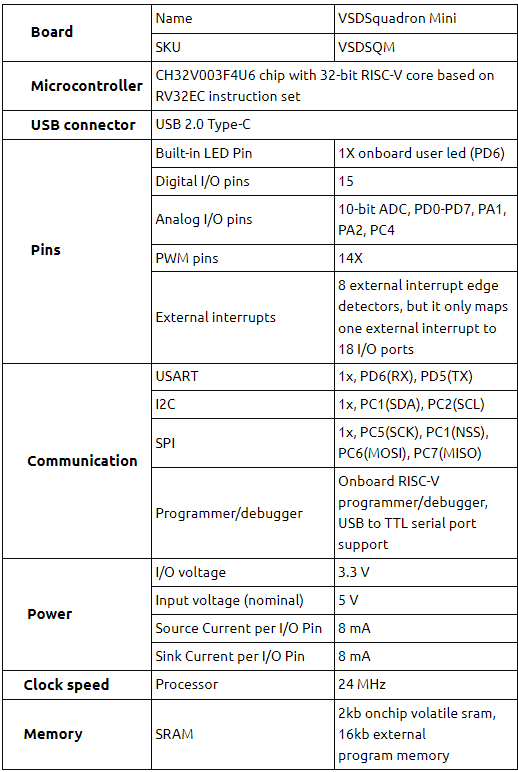
Hello
– In my last post, I was very happy about the robustness of CMOS logic. And here’s more reason to be happy to discover what defines a buffer/inverter as clock cell or regular cell.
This is also, a common question that STA engineers have while hearing about clock path full of clock buffers/inverters. Well, let me try to begin to answer it over here.
In last post, I talked about the robustness of CMOS logic in terms of switching threshold (i.e a voltage at which Vin = Vout), and below table summarizes it all

“On a side note” – it’s always possible to hand-calculate the value of switching threshold, if you know the sizes of transistors. Below image will give a straight forward equation to do that (if it looks complex, donot worry, it has nothing to do with this post, you can safely scroll over :))

Alternatively, if you want to design your CMOS inverter around certain switching threshold, you can do that as well. Below equation will help to obtain the same (Again, if you do not follow this equation, just scroll over:), you can always learn about it in my Circuit design course)

Moving on … If you observe the below table, you will find out, that if PMOS is twice the NMOS in a CMOS inverter, you get the switching threshold close to middle of your supply voltage, and you also get a benefit of equal rise-fall time of that inverter. Same logic applies for buffer as well

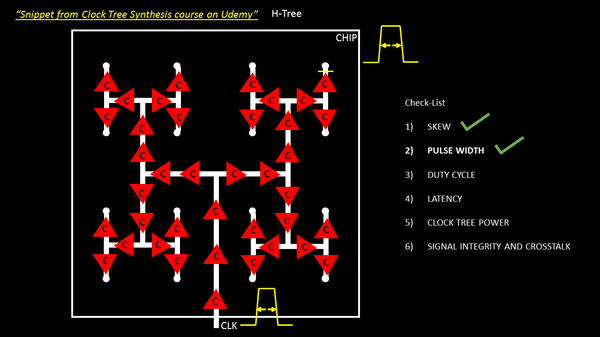
If you recollect the below image from my clock tree synthesis course, where the clock signal from clock port got disturbed at flop clock pin .. (sentence continued after below image)

… (sentence continued from above), I had solved this problem using a clock cell, whose rise-fall delay was exactly (or approximately) the same
I am glad, now you have knowledge what’s a clock cell and how critically its been designed. Also now you know, how important device physics plays role, in overallphysical design flow.
“All our knowledge begins with the senses, proceeds then to the understanding, and ends with reason. There’s nothing higher than reason“ — Immanuel Kant
And this post just did that 🙂
Happy Learning !!