Hello
This is like the ‘Batman’ of static timing analysis. We have heard stories about it but never seen it. The reasons, this comes more from an algorithm point of view.
How about looking a level higher and a level deeper into below timing path?

I will take an example of combinational logic and will convert or represent the combinational logic as Directed Acyclic Graph (DAG) as below. Now DAG is something related more to software, and that’s not our intention here. So I will keep that aside for some time now and focus on actual arrival time (AAT) and required arrival time (RAT).
I am sure you have heard of arrival time and required time. AAT and RAT are of the same class but of a different level and commonly used to denote node times. Stay with me and I will come to that in a moment
First, let’s add cell delays, wire delays and input delays to the combinational logic.

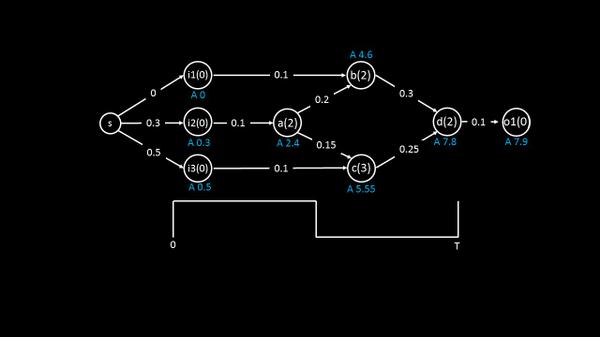
In the above image, a(2) says cell ‘a’ has a delay of 2 units, wire delay from (say) i2 to input of cell ‘a’ is 0.1 units and i2(0.3) represents the time (after launch clock edge) when signal transition occurs. In this case, signal transition occurs at 0.3 time units after launch clock edge.
Now converting the above to DAG takes some amount of work. We use a source node for each input pin like below

The cells are converted to nodes with their delay and cell names shown inside circles …….. (sentence continued below)

…….. (sentence continued from above) and the wire delays are represented as directed arrows like below


For the output pin, we use a node, and represent the delay from output of cell ‘d’ to input of ‘output’ node as below

Above is called the ‘graph’. I still have to introduce ‘timing’ to it, to call this one as a ‘timing graph’. So we found out 30% of ‘timing graph’ hidden story and I can promise you that things become really interesting when we discover the rest 70%.
If you are wondering from where did I get the above images, well, these are from my new (pre)launch course on ‘static timing analysis’ where, including above, I will be introducing you to such cool concepts of timing and make your journey memorable.
“You don’t learn to walk by following rules. You learn by doing, and falling over” – Richard Branson
That’s what I have been doing in all my courses/blogs and will continue doing that.
Happy Learning!!